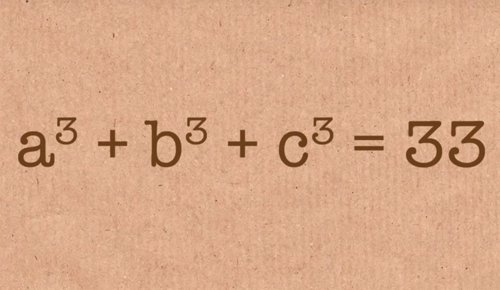
YOUTUBE
MADRID, 2 Abr. (EUROPA PRESS) -
42 es el único número restante (elegible) por debajo de 100 que no ha sido representado como la suma de tres cubos. El reto con el 33 ha sido descifrado por Andrew Bookerm, de la Universidad de Bristol.
Se trata de la solución a parte de un problema matemático de hace 64 años: expresar el número 33 como la suma de tres cubos.
Desde la década de 1950, los matemáticos se han preguntado si todos los números enteros se podrían expresar como la suma de tres cubos; si la ecuación k = x3+ y3+ z3 siempre tiene una solución.
El rompecabezas es una ecuación diofántica en el campo de la teoría de los números y forma parte de uno de los problemas más misteriosos y perversamente difíciles de las matemáticas. Todavía no sabemos la respuesta.
A medida que la potencia de computación ha aumentado, se identificaron más de estas soluciones, así como un grupo que sabemos que no tiene soluciones; aquellos que dejan el resto 4 o 5 cuando se dividen por 9. Hasta hace poco, solo quedaban dos soluciones desconocidas más por debajo de 100; 33 y 42.
Andrew Booker, lector de Matemáticas Puras de la Escuela de Matemáticas de la Universidad, ha descubierto la solución para el número 33: 33: (8,866,128,975,287,528)elevado al cubo + (-8,778,405,442,862,239) elevado al cubo + (-2,736,111,468,807,040) elevado al cubo.
Booker esperaba hacer una búsqueda mucho más extensa, pero la computadora identificó una solución después de un par de semanas. "Tenía una muy buena suposición de que encontraría algo para uno de los números por debajo de 1.000. Pero no sabía que iba a ser el número 33. No sabemos si los números restantes tienen infinitas soluciones, o cómo de frecuentes son esas soluciones. Es bastante misterioso", explica en un comunicado.
Históricamente, la conjetura fue que no existían soluciones para algunos de estos números, que eran imposibles de resolver.
Los matemáticos simplemente no saben si alguna vez podrán responder esto por cada número; podría ser que la suma de los tres cubos sea un problema indecidible o independiente de los axiomas de las matemáticas. Pero cada nuevo descubrimiento proporciona evidencia para la conjetura moderna de que todos los números elegibles tienen soluciones.
"Esto está justo en el límite entre lo que sabemos cómo probar y lo que sospechamos que podría ser indecidible", opina.
El siguiente y último número no resuelto debajo de 100, 42, tiene el atractivo de ser la respuesta de Douglas Adams al significado de la vida. Booker está trabajando actualmente con Andrew Sutherland del MIT para encontrarlo.